Angular Momentum and Conservation of Angular Momentum

A particle moves in a circular path with constant speed. Find out a point about which the angular momentum of the particle is constant and another point about which it changes with time.

 A cat is at rest on a horizontal table mounted on a vertical axis. If the cat begins to walk around the perimeter, what happens to the table ?  Explain.

"It is easier to keep your balance on a moving bicycle than on a bicycle at rest ". Why ?

The torque acting on a particle about an arbitrary origin is zero, what can you say about its angular momentum?

Explain the law of conservation of angular momentum.

Write down the relation connecting torque and angular momentum ?

What is the S.I. unit and dimensional formula of angular momentum?

How is the angular momentum of a rigid body related to its moment of inertia?

An electron moves around the nucleus of an atom, in a circular path. What is the direction of the angular momentum of the electron?

Calculate the angular momentum and rotational kinetic energy of the earth about its own axis. Given mass of the earth is $6\times {10}^{24} \mathrm{kg}$ and its radius$=6.4\times {10}^3 \mathrm{km}$ [Moment of inertia of the earth about its axis of rotation is $\frac{2}{5}m{r}^2$]

A heavy circular disc is revolving in a horizontal plane about the centre which is fixed. An insect of mass $\frac{1}{n}th$  that of the disc walks from the centre along a radius and then flies away. Show that the final angular velocity is $\frac{n}{n+2}$ times the original angular velocity of the disc.

The mass of a star is $3.98\times {10}^{30} \mathrm{kg}$ and its radius is ${10}^6 \mathrm{km}$. It rotates about its axis with an angular speed of ${10}^{-6} \mathrm{rad} {\mathrm{s}}^{-1}$. Calculate the speed of the star when it collapses to a radius of ${10}^4 \mathrm{km}$?  Assume the moment of inertia of the star to be $\frac{2}{5}m{r}^2$.

The maximum and minimum distance of a comet from the sun are $1.4\times {10}^{12} \mathrm{m}$  and $7\times {10}^{10} \mathrm{m}$. If its velocity nearest to the sun is $6\times {10}^4 \mathrm{m} {\mathrm{s}}^{-1}$, what is the velocity in the farthest position?  Assume a circular path for the comet.

If earth suddenly contracts by $\frac{1}{2}$ of its present radius by how much would the day be decreased?

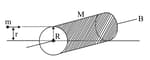
A small body of mass $100 \mathrm{g}$ moving with a velocity $2 \mathrm{m} {\mathrm{s}}^{-1}$ is strikes a solid cylinder of mass $2 \mathrm{kg}$ and radius $20 \mathrm{cm}$. The cylinder is initially at rest and is mounted on a fixed horizontal axle that passes through the centre of mass. The line of motion of the small body is at a perpendicular distance of $15 \mathrm{cm}$ from the centre of the cylinder. The small body strikes the cylinder and adheres to its surface. What is the angu­lar speed of the system just after the collision? Assume there is no friction.

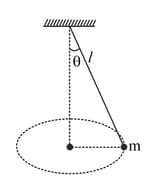
The figure shows a conical pendulum. If the length of the pendulum is $l$, mass of the bob is $m$ and $\theta$ is the angle made by the string with the vertical show that the angular momentum of the pendulum about the point of support is $L=\sqrt{\frac{m^{2}g{l}^3{\sin }^4\theta }{\cos \theta }}$

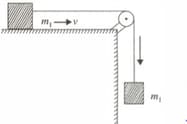
If $m_1=3 \mathrm{kg}$ and $m_2=1 \mathrm{kg}$ what is the angular momentum of the system? The radius of the pulley is $0.3 \mathrm{m}$ and its moment of inertia about its axle is $0.14 \mathrm{kg} {\mathrm{m}}^2$. The system moves with a linear velocity of $2 \mathrm{m} {\mathrm{s}}^{-1}$ is on a frictionless horizontal surface?

Two masses $m_1$ and $m_2$ are connected by a rigid rod of length $l$ and negligible mass. The system rotates about an axis passing through the centre of mass of the system and perpendicu­lar to the length of the rod. Show that the angular momentum of the system is $\mu l^2\omega$ where $\mu =\frac{m_1{m}_2}{m_1+m_2}$

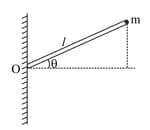
A ball of mass $m$ is attached to light weight rod of length $l$ and held as shown in figure.  Initially it is at rest. If the ball starts to fall, what is its angular momentum as a function of time about the point $O$. Assume that there is no air resistance.

State and prove the law of conservation of angular momentum.